Standard Form of a Line

by Justin Skycak on

Standard form makes it easy to see the intercepts of a line.

This post is a chapter in the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Standard Form of a Line. Justin Math: Algebra. https://justinmath.com/standard-form-of-a-line/

The standard form of a linear equation is $ax+by=c$, where $a$, $b$, and $c$ are all integers and $a$ is nonnegative.

For example, we can convert the equation $y=\frac{3}{5}x+\frac{10}{3}$ to standard form by moving $x$ and $y$ to the same side and multiplying to cancel out any fractions.

$\begin{align*} \text{Given equation} \hspace{.5cm} &\Bigg| \hspace{.5cm} y=\frac{3}{5}x+\frac{10}{3} \\ \text{Subtract } \frac{3}{5}x \text{ from both sides} \hspace{.5cm} &\Bigg| \hspace{.5cm} -\frac{3}{5}x+y=\frac{10}{3} \\ \begin{matrix} \text{Multiply both sides by } 15 \text{, the least} \\ \text{common multiple of } 5 \text{ and } 3 \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} -9x+15y=50 \\ \begin{matrix} \text{Multiply both sides by } -1 \text{ to make} \\ \text{the } x \text{ coefficient positive} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} 9x-15y=-50 \end{align*}$


Finding the Intercepts

Standard form makes it easy to see the intercepts of the line: to get the x-intercept in $ax+by=c$, we divide the constant $c$ by the x-coefficient $a$, and to get the y-intercept, we divide the constant $c$ by the y-coefficient $b$.

For example, the x-coefficient of $9x-15y=-50$ is $-\frac{50}{9}$, and the y-coefficient is $\frac{-50}{-15}$ which simplifies to $\frac{10}{3}$.

This trick for finding the intercepts works because finding the intercept of a particular variable involves substituting $0$ for the other variable. The x-intercept occurs at some point $(x,0)$ where $y$ is $0$, so to solve for the x-intercept, we can substitute $0$ for $y$ and solve for $x$.

$\begin{align*} \text{Given equation} \hspace{.5cm} &\Bigg| \hspace{.5cm} ax+by=c \\ \text{Substitute } 0 \text{ for } y \hspace{.5cm} &\Bigg| \hspace{.5cm} ax+b(0)=c \\ \text{Simplify} \hspace{.5cm} &\Bigg| \hspace{.5cm} ax=c \\ \text{Divide by } a \hspace{.5cm} &\Bigg| \hspace{.5cm} x=\frac{c}{a} \end{align*}$


Likewise, the y-intercept occurs at some point $(0,y)$ where $x$ is $0$, so to solve for the y-intercept, we can substitute $0$ for $x$ and solve for $y$.

$\begin{align*} \text{Given equation} \hspace{.5cm} &\Bigg| \hspace{.5cm} ax+by=c \\ \text{Substitute } 0 \text{ for } x \hspace{.5cm} &\Bigg| \hspace{.5cm} a(0)+by=c \\ \text{Simplify} \hspace{.5cm} &\Bigg| \hspace{.5cm} by=c \\ \text{Divide by } a \hspace{.5cm} &\Bigg| \hspace{.5cm} y=\frac{c}{b} \end{align*}$


Graphing

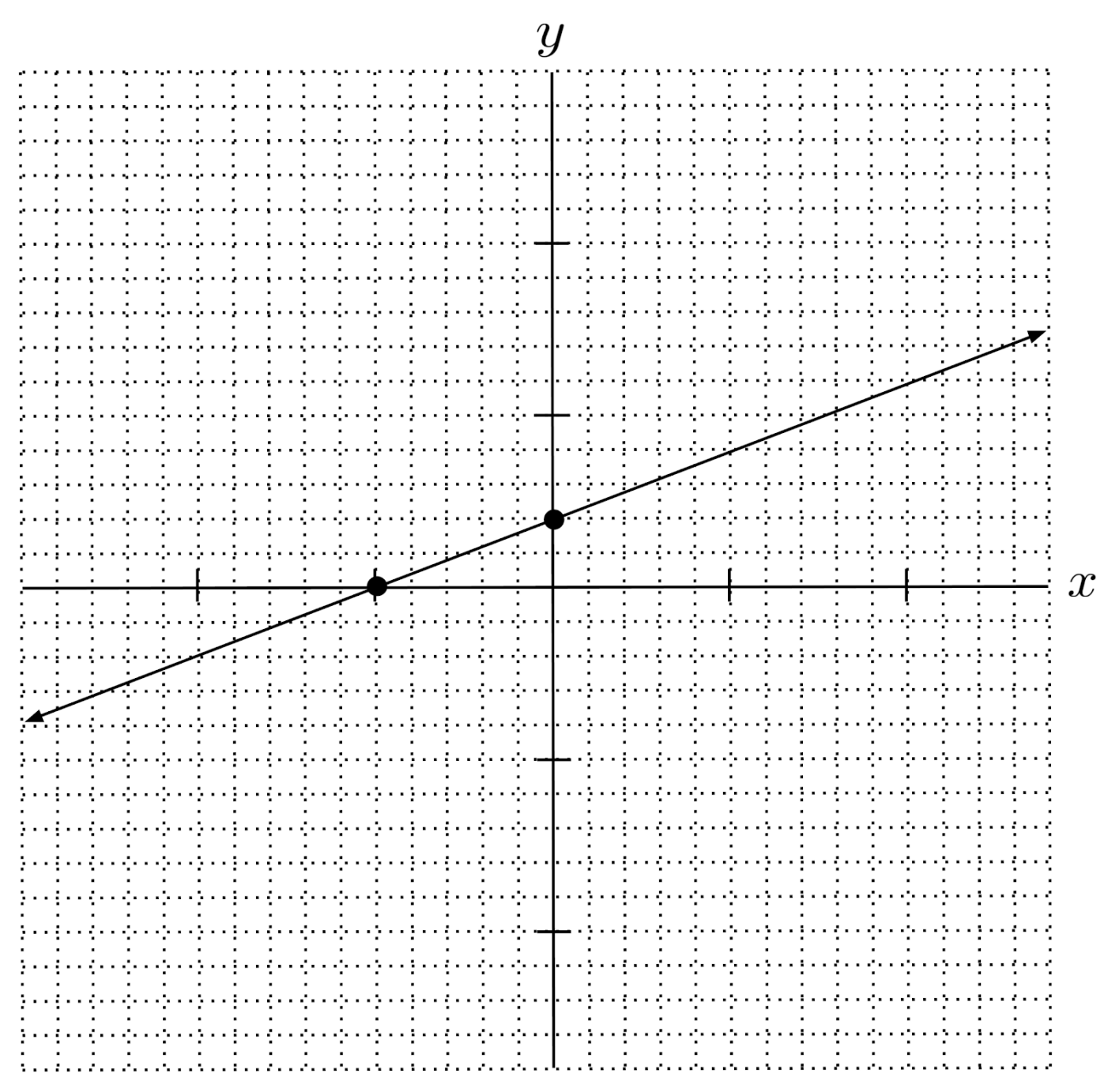
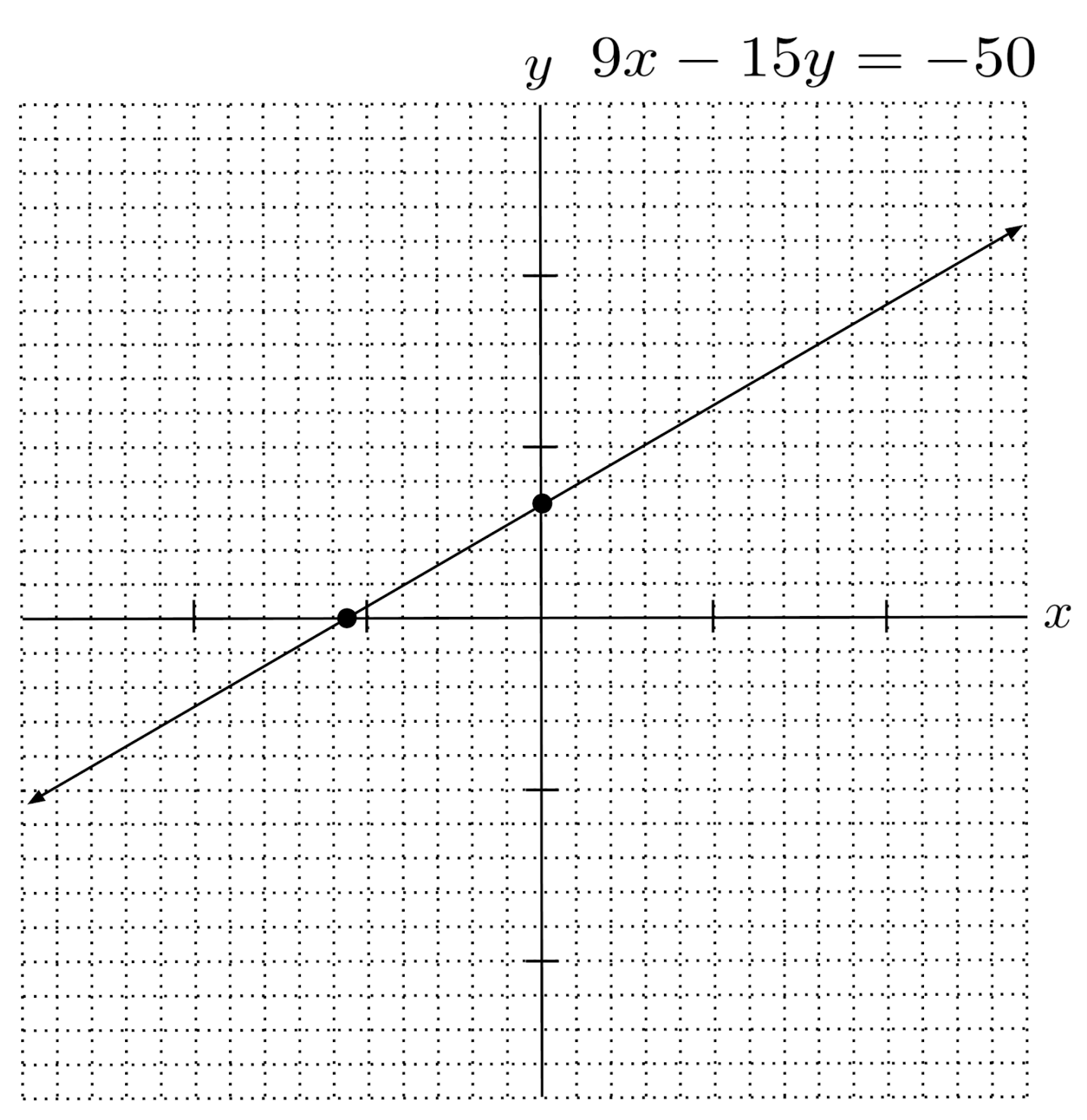
To plot the line, then, all we have to do is mark the intercepts and then draw a line through them.

For example, in the line $9x-15y=-50$, we computed the x-intercept as $-\frac{50}{9}$, or $-5 \frac{5}{9}$, and the y-intercept as $\frac{10}{3}$, or $3 \frac{1}{3}$.

To graph the line, we just need to plot the intercepts $\left( -5 \frac{5}{9},0 \right)$ and $\left( 0,3 \frac{1}{3} \right)$ and draw a line through them.

icon


Exercises

Write the equation in standard form. (You can view the solution by clicking on the problem.)

$1) \hspace{.5cm} y=\frac{3}{4}x-1$
Solution:
$3x-4y=4$

$2) \hspace{.5cm} -2x+3y=4$
Solution:
$2x-3y=-4$

$3) \hspace{.5cm} \frac{1}{3}x - y = 2$
Solution:
$x-3y=6$

$4) \hspace{.5cm} 5x-4y=1$
Solution:
$5x-4y=1$

$5) \hspace{.5cm} y+x=2$
Solution:
$x+y=2$

$6) \hspace{.5cm} 4x+y=\frac{1}{3}$
Solution:
$12x+3y=1$


Graph the following by drawing a line through the intercepts. (You can view the solution by clicking on the problem.)

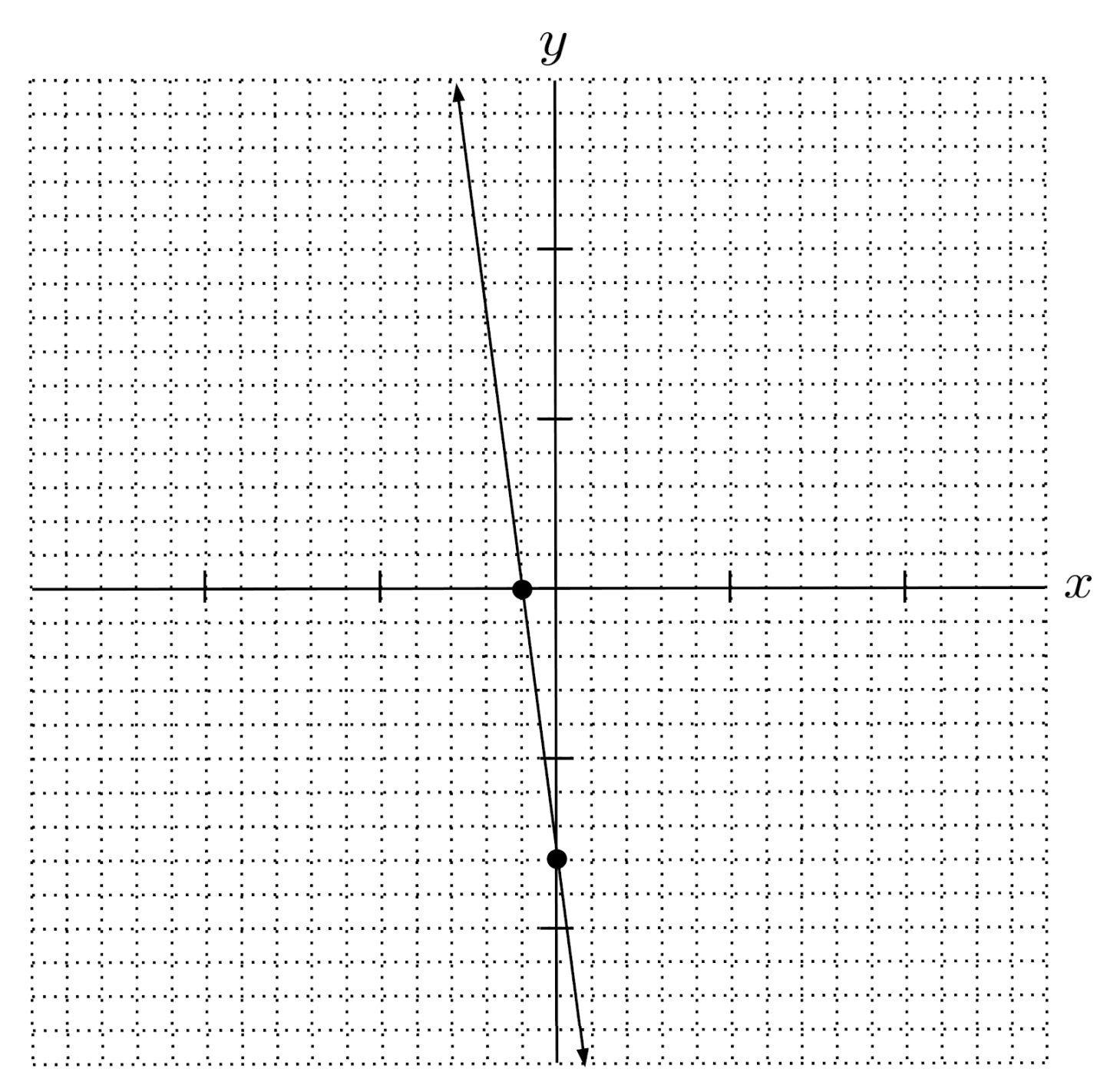
$7) \hspace{.5cm} y-2=3(x-4)$
Solution:
icon

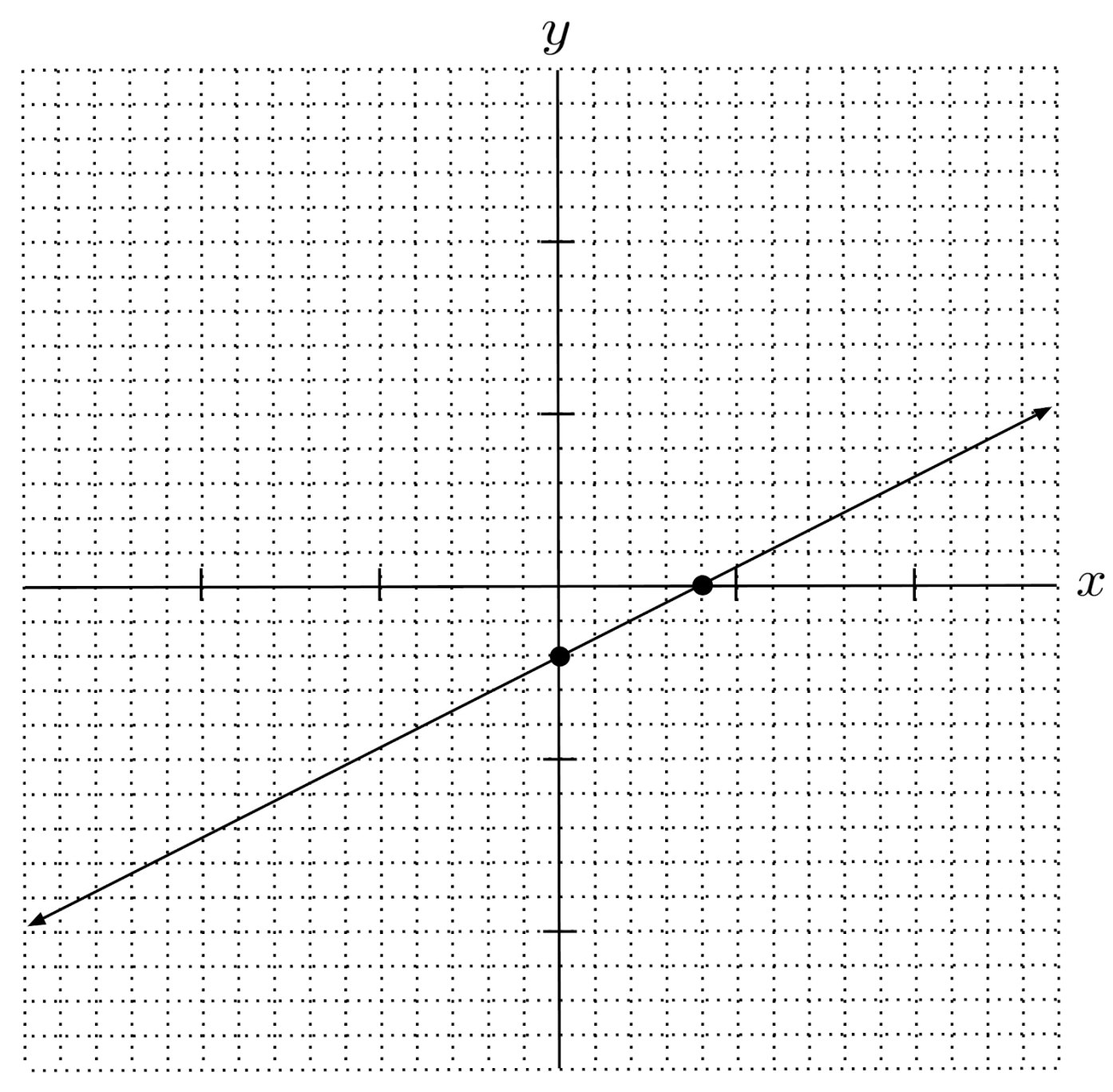
$8) \hspace{.5cm} y+7=-2(x-2)$
Solution:
icon

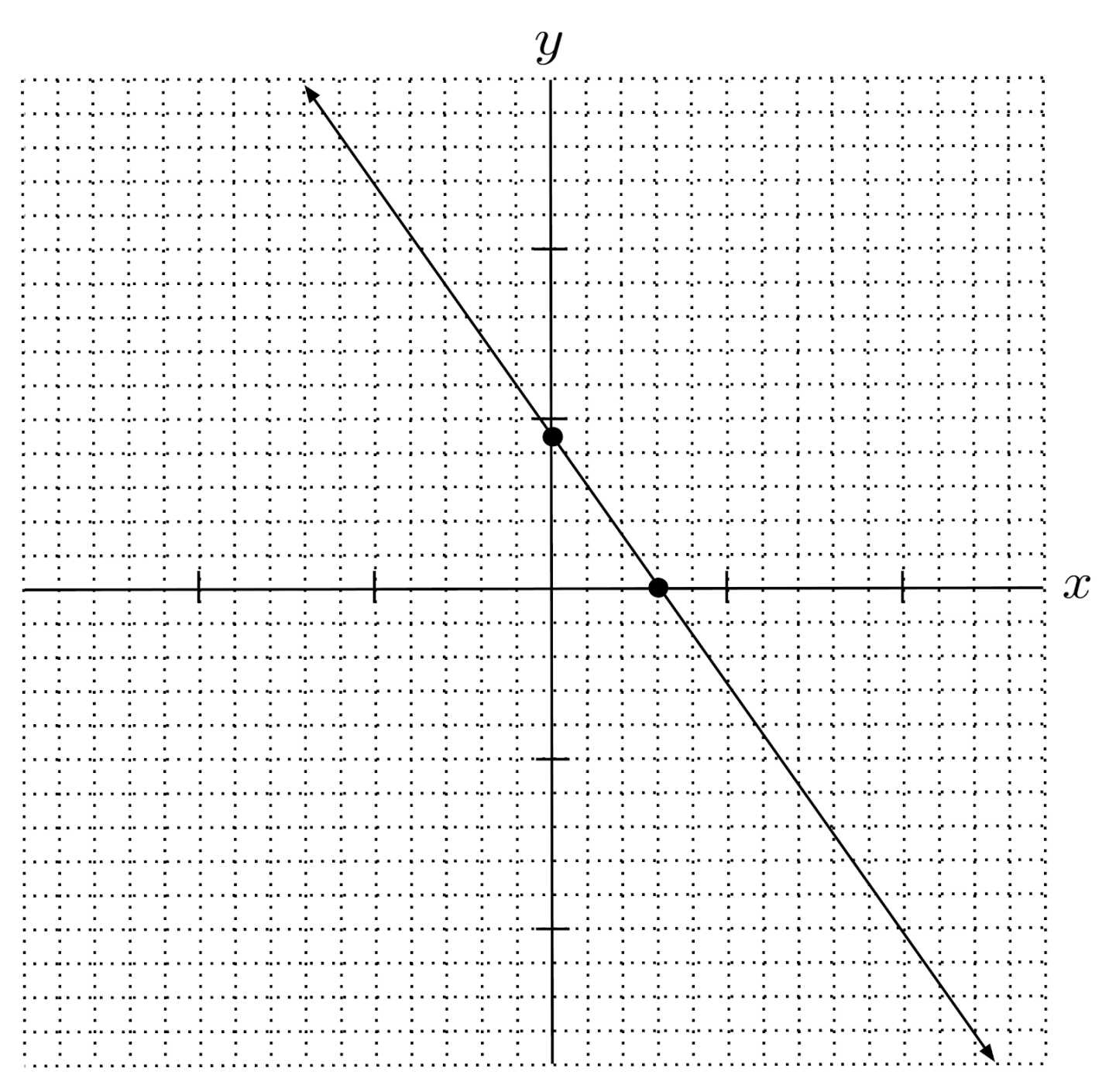
$9) \hspace{.5cm} y-\frac{1}{2} = \frac{1}{3}(x+1)$
Solution:
icon

$10) \hspace{.5cm} y+\frac{5}{2} = -\frac{2}{5}\left( x-\frac{1}{4} \right)$
Solution:
icon

This post is a chapter in the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Standard Form of a Line. Justin Math: Algebra. https://justinmath.com/standard-form-of-a-line/